在本課中,我們將探索加密貨幣市場的獨特特性,並學習如何使用現代投資組合理論(MPT)來優化加密貨幣組合。我們還將深入探討優化算法,如蒙特卡洛模擬和遺傳算法,提供詳細的公式和實際示例,以增強我們的資產配置策略。最後,我們將使用Python和加密貨幣交易所的API來實現我們的交易策略。今日 Colab

期望收益:基於歷史數據的平均預期收益。
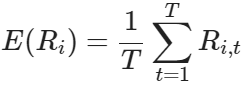
E(R_i):資產 i 的期望收益R_{i,t}:資產 i 在時間 t 的收益T:總觀測期數協方差矩陣:衡量資產收益如何共同變動。
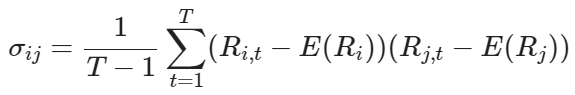
\sigma_{ij}:資產 i 和 j 的協方差在本節中,我們將深入探討如何使用優化算法來改進加密貨幣投資組合的資產配置。我們將詳細介紹蒙特卡洛模擬和遺傳算法,並提供數學公式和實際示例,幫助您理解這些技術如何應用於投資組合優化。
蒙特卡洛模擬是一種利用隨機抽樣和統計模型來估計數學問題解決方案的方法。它特別適用於複雜的、多變量的問題,如投資組合優化。
目標:通過隨機生成大量的資產權重組合,計算每個組合的預期收益和風險,從而找到最優的投資組合。
投資組合的預期收益:
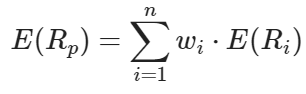
E(R_p):投資組合的預期收益w_i:資產 i 的權重E(R_i):資產 i 的期望收益n:資產的數量投資組合的風險(標準差):
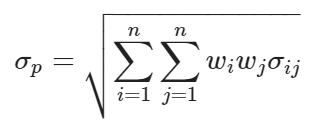
\sigma_p:投資組合的標準差\sigma_{ij}:資產 i 和資產 j 之間的協方差夏普比率:
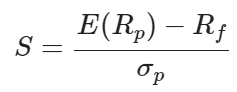
S:夏普比率R_f:無風險利率假設:我們有三種加密貨幣資產:BTC、ETH 和 LTC。
步驟:
收集歷史價格數據:獲取過去一年的每日收盤價。
計算每日收益率:使用價格數據計算每日收益率。
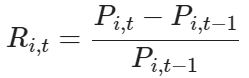
R_{i,t}:資產 i 在時間 t 的收益率P_{i,t}:資產 i 在時間 t 的價格計算平均收益和協方差矩陣:
我們將創建一個假設值包含 5 天收益率的 DataFrame,數據為假設的每日收益率。
import numpy as np
import pandas as pd
# 創建日期索引
dates = pd.date_range('2022-01-01', periods=5)
# 創建假設的每日收益率數據(以百分比表示)
data = {
'BTC': [0.02, -0.015, 0.01, 0.005, -0.01],
'ETH': [0.025, -0.02, 0.015, 0.007, -0.012],
'LTC': [0.015, -0.01, 0.005, 0.003, -0.008]
}
# 創建 DataFrame
returns = pd.DataFrame(data, index=dates)
print("資產收益率 DataFrame:")
print(returns)
我們用這個資料來做以下計算
import numpy as np
import pandas as pd
# 假設 returns 是資產收益率的 DataFrame
mean_returns = returns.mean()
cov_matrix = returns.cov()
進行蒙特卡洛模擬:
num_portfolios = 50000
results = np.zeros((3, num_portfolios))
weights_record = []
for i in range(num_portfolios):
# 隨機生成資產權重
weights = np.random.random(3)
weights /= np.sum(weights)
weights_record.append(weights)
# 計算投資組合收益和風險
portfolio_return = np.sum(mean_returns * weights)
portfolio_std_dev = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
# 計算夏普比率(假設無風險利率為 0)
sharpe_ratio = portfolio_return / portfolio_std_dev
# 保存結果
results[0,i] = portfolio_std_dev
results[1,i] = portfolio_return
results[2,i] = sharpe_ratio
繪製有效前沿:
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 7))
plt.scatter(results[0,:], results[1,:], c=results[2,:], cmap='viridis')
plt.xlabel('風險(標準差)')
plt.ylabel('預期收益')
plt.colorbar(label='夏普比率')
plt.show()
可以得到以下圖形: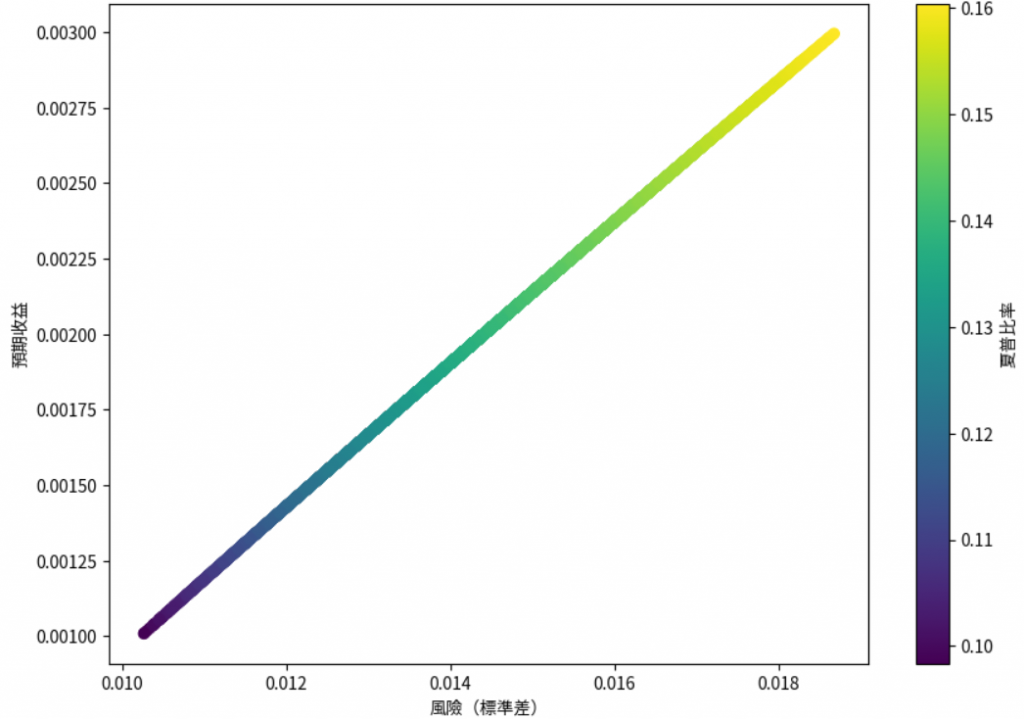
找到最優投資組合:
# 將結果轉換為 DataFrame 以便於查看
results_frame = pd.DataFrame(results.T, columns=['標準差', '預期收益', '夏普比率'])
# 找到夏普比率最大的投資組合
max_sharpe_idx = results_frame['夏普比率'].idxmax()
optimal_std_dev = results_frame.loc[max_sharpe_idx, '標準差']
optimal_return = results_frame.loc[max_sharpe_idx, '預期收益']
optimal_weights = weights_record[max_sharpe_idx]
print("最優投資組合權重:")
print("BTC:", round(optimal_weights[0], 4))
print("ETH:", round(optimal_weights[1], 4))
print("LTC:", round(optimal_weights[2], 4))
print("\n對應的預期收益:", round(optimal_return, 4))
print("對應的風險(標準差):", round(optimal_std_dev, 4))
print("對應的夏普比率:", round(results_frame.loc[max_sharpe_idx, '夏普比率'], 4))
可以得到:

解釋:
遺傳算法(Genetic Algorithm)是一種模仿自然進化過程的隨機搜索算法。它通過選擇、交叉和變異等操作,不斷優化候選解,以找到全局最優解。
目標:優化資產權重,使投資組合的夏普比率最大化。
初始種群:隨機生成一組投資組合(個體),每個個體由資產權重組成。
適應度評估:計算每個個體的適應度函數(例如,夏普比率)。
選擇:根據適應度選擇優秀的個體作為父代。
交叉:結合兩個父代個體的特徵,產生新的子代個體。
變異:對子代個體進行隨機變異,以增加多樣性。
更新種群:將子代個體加入種群,並根據適應度選擇下一代種群。
重複步驟 2-6,直到滿足停止條件(如達到最大代數或適應度不再提升)。
適應度函數(以夏普比率為例):
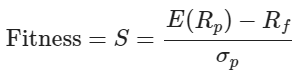
E(R_p):投資組合的預期收益\sigma_p:投資組合的標準差R_f:無風險利率我們將使用與蒙特卡洛模擬相同的示例數據,來展示如何應用遺傳算法進行投資組合優化。
我們已經有了資產收益率 DataFrame returns、平均收益 mean_returns 和協方差矩陣 cov_matrix。
# returns, mean_returns, cov_matrix 已在前面計算
我們將使用 DEAP 庫來實現遺傳算法。官網

from deap import base, creator, tools, algorithms
# 定義評估函數,目標是最大化夏普比率
def evaluate_individual(individual):
weights = np.array(individual)
portfolio_return = np.sum(mean_returns * weights)
portfolio_std_dev = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
if portfolio_std_dev == 0:
return 0,
sharpe_ratio = portfolio_return / portfolio_std_dev
return sharpe_ratio,
# 創建 Fitness 和 Individual 類型
creator.create('FitnessMax', base.Fitness, weights=(1.0,))
creator.create('Individual', list, fitness=creator.FitnessMax)
# 設置工具箱
toolbox = base.Toolbox()
toolbox.register('attr_float', np.random.random)
# 定義個體:隨機生成權重,並確保總和為 1
def create_individual():
weights = [np.random.random() for _ in range(len(mean_returns))]
total = sum(weights)
weights = [w / total for w in weights]
return creator.Individual(weights)
toolbox.register('individual', create_individual)
toolbox.register('population', tools.initRepeat, list, toolbox.individual)
# 遺傳操作
toolbox.register('evaluate', evaluate_individual)
toolbox.register('mate', tools.cxBlend, alpha=0.5)
toolbox.register('mutate', tools.mutGaussian, mu=0, sigma=0.1, indpb=0.2)
toolbox.register('select', tools.selTournament, tournsize=3)
# 參數設置
population_size = 50
num_generations = 50
crossover_prob = 0.7
mutation_prob = 0.2
# 初始化種群
population = toolbox.population(n=population_size)
# 記錄最優解
hall_of_fame = tools.HallOfFame(1)
# 統計信息
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("max", np.max)
stats.register("avg", np.mean)
# 運行遺傳算法
population, logbook = algorithms.eaSimple(population, toolbox, cxpb=crossover_prob, mutpb=mutation_prob,
ngen=num_generations, stats=stats, halloffame=hall_of_fame, verbose=True)
輸出示例:
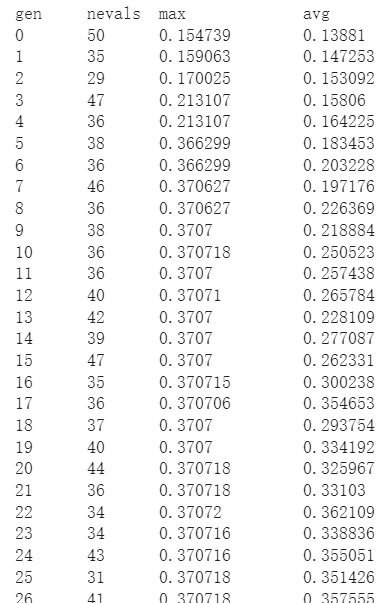
# 最優個體
best_individual = hall_of_fame[0]
optimal_weights = np.array(best_individual)
portfolio_return = np.sum(mean_returns * optimal_weights)
portfolio_std_dev = np.sqrt(np.dot(optimal_weights.T, np.dot(cov_matrix, optimal_weights)))
sharpe_ratio = portfolio_return / portfolio_std_dev if portfolio_std_dev != 0 else 0
print("最優投資組合權重:")
print("BTC:", round(optimal_weights[0], 4))
print("ETH:", round(optimal_weights[1], 4))
print("LTC:", round(optimal_weights[2], 4))
print("\n對應的預期收益:", round(portfolio_return, 4))
print("對應的風險(標準差):", round(portfolio_std_dev, 4))
print("對應的夏普比率:", round(sharpe_ratio, 4))
輸出示例(結果可能因隨機性而異):
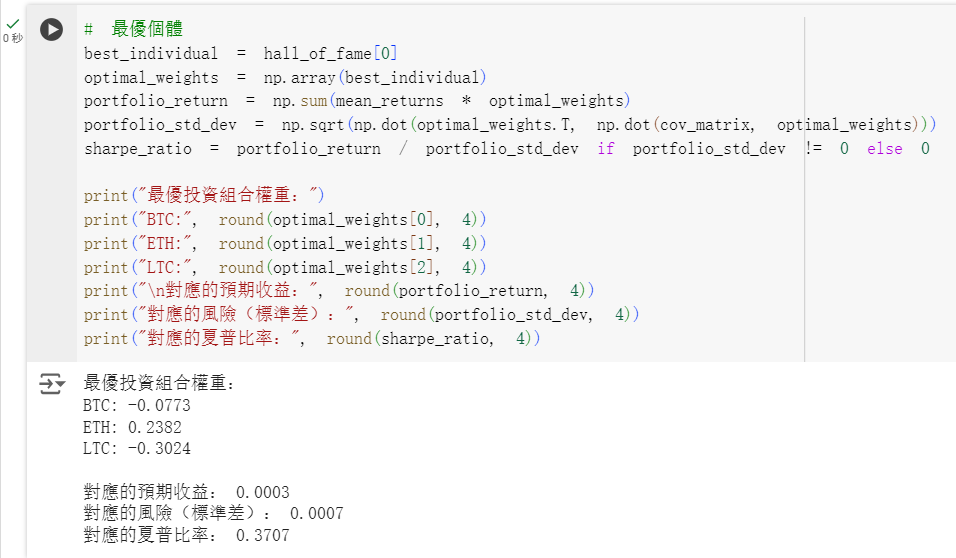
解釋:

ccxt庫:
import ccxt
import pandas as pd
exchange = ccxt.binance()
symbols = ['BTC/USDT', 'ETH/USDT', 'LTC/USDT']
data = {}
for symbol in symbols:
ohlcv = exchange.fetch_ohlcv(symbol, timeframe='1d', limit=365)
df = pd.DataFrame(ohlcv, columns=['timestamp', 'open', 'high', 'low', 'close', 'volume'])
df['timestamp'] = pd.to_datetime(df['timestamp'], unit='ms')
df.set_index('timestamp', inplace=True)
data[symbol] = df['close']
prices = pd.DataFrame(data)
returns = prices.pct_change().dropna()
mean_returns = returns.mean()
cov_matrix = returns.cov()
import numpy as np
from scipy.optimize import minimize
def portfolio_performance(weights, mean_returns, cov_matrix):
returns = np.sum(mean_returns * weights)
std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
return std, returns
def negative_sharpe_ratio(weights, mean_returns, cov_matrix, risk_free_rate=0):
std, returns = portfolio_performance(weights, mean_returns, cov_matrix)
sharpe_ratio = (returns - risk_free_rate) / std
return -sharpe_ratio
num_assets = len(symbols)
args = (mean_returns, cov_matrix)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bounds = tuple((0,1) for asset in range(num_assets))
result = minimize(negative_sharpe_ratio, num_assets*[1./num_assets,], args=args,
method='SLSQP', bounds=bounds, constraints=constraints)
optimal_weights = result.x
(此部分已在第四節詳細介紹)
(此部分已在第四節詳細介紹)
ccxt的示例:symbol = 'BTC/USDT'
amount = 0.001 # 示例數量
order = exchange.create_order(symbol, 'market', 'buy', amount)
print(order)
exchange.apiKey = '您的API密鑰'
exchange.secret = '您的秘密密鑰'
通過本課的學習,應該對如何將投資組合優化技術應用於加密貨幣,以及如何使用Python和交易所API實現這些策略有了扎實的理解。
